XGBoost: A Scalable Tree Boosting System

Chen and Guestrin (2016)

Christian Bager Bach Houmann

22 Sep 2023

By the end of this talk…

You should understand every word of

XGBoost: A Scalable Tree Boosting

And why you should use XGBoost!

Let’s try it!

• Using the IRIS dataset from Scikit-Learn: small dataset with iris (flower) data
• We get very good classifications out of the box

from xgboost import XGBClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

data = load_iris()
X_train, X_test, y_train, y_test = train_test_split(
    data['data'], data['target'], 
    test_size=.2, random_state=42
)
bst = XGBClassifier()

bst.fit(X_train, y_train)
preds = bst.predict(X_test)

Background

From Zero to Gradient Boosting

Supervised Learning

• Supervised learning is where your training data has the desired solutions (labels).
• The model learns a function that maps inputs to correct outputs, which it can use on new, unlabled data to make accurate predictions.

Taken from 5th semester MI course at AAU

Defining an objective

• How do we measure how well the model fit the data? \[ obj(\theta)=L(\theta)+\Omega(\theta) \]
• Objective function = training loss + regularization term
• Training loss: how predictive our model is
• Regularization: helps prevent overfitting by penalizing complexity
• The goal: a simple yet predictive model

\(\theta\) are model parameters, \(L\) is the loss function, and \(\Omega\) is the regularization term.

Decision Trees

XGBoost uses CART: Classification and Regression Trees. I show decision trees to illustrate.

These are different from decision trees in that there is a real score associated with each leaf. The leaf only contains this decision value. So the leaf scores are continuous!

Taken from 5th semester MI course at AAU.

Ensemble Learning

• Simple models like Decision Trees and Linear Regression are limited
• We can boost performance with ensemble learning
• Instead of creating complex model:
  • Create lots of simple models (w. weak learners)
  • Combine them into a meta-model
• The output is a weighted voting of the output from each simple model

Weak learners are learning algorithms that cannot learn complex models, so they are typically fast at training and prediction time.

The most frequently used weak learner is a Decision Tree learning algorithm that we often stop splitting the training set after few iterations.

The trees we get out are shallow and not very accurate, but still better than random guessing, so the combined model is a lot better.

Boosting

We can boost by sequentially training and combining weak learners, each trying to correct its predecessor.

1. Start with a weak learner
2. Calculate the errors of this initial model
3. Fit another weak learner, this time focusing on the errors made by the previous model
4. Combine the weak models through weighted averaging
5. Repeat 2-4 until we have enough models or no further improvements can be made

Boosting

Boosting is where you learn \(F(x)\) as the sum of \(M\) weak learners. \[ F(x)=\sum^{M}_{i=1}f_{i}(x) \]

where \(f_{i}(x)\) is the weak learner.

Gradient Boosted Trees

• Same as boosting, except:
• Instead of fitting to errors from prev. trees, we fit to the negative gradients w.r.t the prediction of the prev. trees.

These negative gradients represent the direction in which the model should change its predictions to minimize the loss.

The use of gradient descent as an optimization framework also sets it apart from other boosting algorithms.

The original paper on Gradient Boosting is by Friedman (2001).

eXtreme Gradient Boosting

Putting it all together…

Contributions

• Scalable, end-to-end tree boosting system¹
• Theoretically justified weighted quantile sketch for efficient proposal calculation²
• Sparsity-aware algorithm for parallel tree learning³
• Cache-aware block structure for out-of-core tree learning⁴

• Scalable: it works well with large datasets
• End-to-end: this is true, but not in the same way deep learning algorithms are end-to-end - they can take raw images/raw text, xgb cannot
• Weighted quantile sketch: this is what makes xgboost faster and more accurate than some other gradient boosting algorithms
• Sparsity-aware: this is also useful for high dimensionality data with missing values
• Parallel: both parallel computation during tree construction and boosting rounds
• Cache aware: is because XGBoost has hardware-optimized data structures that are cache efficient.
• Out-of-core: XGBoost doesn’t use online learning - for XGBoost, this happens by storing data in binary files and loading chunks during learning.

1. End-to-end means it takes raw input and produces final output - no relying on intermediary or hand-coded steps

2. It’s efficient at finding optimal splits

3. Sparsity means not all values are stored - e.g. \(0\)s or NULLs are not in \(X\) training data

4. Out-of-core means that we learn (via online learning) on mini-batches of training data.

How XGBoost learns trees

Our model is of the form

\[ \hat{y}_{i}=\sum^{K}_{k=1}f_{k}(x_{i}),\quad f_{k}\in\mathcal{F} \]

where

• \(K\) is the number of trees,
• \(f_k\) is a function in the functional space \(\mathcal{F}=\{ f(x)=w_{q(x)} \}\), which is the set of all possible CARTs,
• \(q\) maps a sample to a leaf,
• and \(w_j\) is the weight for a leaf \(j\).

How XGBoost learns trees

The idea is we try to optimize

\[ obj(\theta)=\sum^{n}_{i}l(y_{i},\hat{y}_{i})+\sum^{K}_{k=1}\omega(f_{k}) \] where \(\omega(f_{k})\) is the complexity of the tree \(f_{k}\).

But… how do we actually learn the trees? What about their structure and leaf scores?

Unfortunately, it’s not as easy as just optimizing this function.

We need to learn the functions \(f_i\) which each contains the structure of the tree and leaf scores.

As you may recall: objective function = loss function + regularization term.

I’ll talk about the complexity later.

How XGBoost learns trees

We learn the trees additively!

\[ \begin{align} &\hat{y}^{(0)}_{i}=0 \\ &\hat{y}^{(1)}_{i}=f_{1}(x_{i})=\hat{y}_{i}^{(0)}+f_{1}(x_{i}) \\ &\hat{y}^{(2)}_{i}=f_{1}(x_{i})+f_{2}(x_{i})=\hat{y}_{i}^{(1)}+f_{2}(x_{i}) \\ &\quad\cdots \\ & \hat{y}^{(t)}_{i}=\sum^{t}_{k=1}f_{k}(x_{i})=\hat{y}_{i}^{(t-1)}+f_{t}(x_{i}) \end{align} \]

So the prediction is going to be the sum of all tree functions, which is the same as all the previous predictions + our latest tree’s prediction.

How do we know which tree we want at each step?

The one that optimizes our objective:

\[ \begin{align} obj(t) &= \sum^{n}_{i=1}l(y_{i},\hat{y}^{(t)}_{i})+\sum^{t}_{i=1}\omega(f_{i}) \\ &=\sum^{n}_{i=1}l(y_{i},\hat{y}^{(t-1)}_{i}+f_{t}(x_{i}))+\omega(f_{t})+\text{constant} \end{align} \]

However, we can’t optimize this objective function with traditional methods in Euclidean space - because our model takes functions as parameters.

So we approximate it with Taylor expansion to the second-order to optimize for the general loss functions.

This makes it possible to optimize as there are some loss functions you otherwise couldn’t optimize – we make it general, so you can use arbitrary loss functions, as long as they are differentiable.

And what about the regularization term?

Remember our definition of a tree: \[ f_{t}(x)=w_{q(x)},\quad w\in \mathbb{R}^{T}, q:\mathbb{R}^{d}\rightarrow \{1,2,\dots ,T\} \] \(w\) is the vector score on leaves, \(q\) is a function that assign each data point to the corresponding leaf, and \(T\) is the number of leaves.

We define the complexity as \[ \omega(f)=\gamma T+ \frac{1}{2}\lambda \sum^{T}_{j=1}w^{2}_{j} \]

Now that we know the training step, we need to define the regularization

\(\gamma\) is the minimum gain to make a split, which helps us prevent the model from making too many splits unless they improve the fit.

\(\lambda\) is to regularize the leaf weights. They capture some pattern from the training data, but if they’re too large/too small, the model might fit the data too closely - we don’t want it to remember all the noise. If \(\lambda\) is too large we might underfit because the weights are too small.

So our complexity measure just regulates our model based on how many leaves it makes and ensures the weights don’t get out of control.

Learning the tree structure

Use the Exact Greedy Algorithm:

1. Start with single root - contains all training examples
2. Iterate over all features and values per feature¹ and evaluate each possible split gain
3. Output split with best score

The gain for the best split must be positive, otherwise we stop growing the branch

START HERE

• Cannot enumerate all possible tree structures…
• So we find the best tree by optimizing one level at a time

The algorithm here is the Exact Greedy Algoritm we use.

AFTER SLIDE Let’s review the gain.

I’m skipping how we derive the structure function from the objective function

1. Must be sorted

Gain

We try to split a leaf into two leaves, and the score it gains is \[ Gain=\frac{1}{2}\left[ \frac{G^{2}_{L}}{H_{L}+\lambda}+ \frac{G^{2}_{R}}{H_{R}+\lambda}-\frac{(G_{L}+G_{R})^{2}}{H_{L}+H_{R}+\lambda} \right]-\gamma \]

1. The score on the new left leaf
2. The score on the new right leaf
3. The score if we do not split
4. The complexity cost by adding additional leaf

First: gain is loss reduction - so it’s a measure of whether we actually improve the model by splitting.

1. The score on the new left leaf \(\frac{G^{2}_{L}}{H_{L}+\lambda}\)
2. The score on the new right leaf \(\frac{G^{2}_{R}}{H_{R}+\lambda}\)
3. The score if we do not split \(\frac{(G_{L}+G_{R})^{2}}{H_{L}+H_{R}+\lambda}\)
4. The complexity cost by adding additional leaf \(\gamma\)

If the gain is smaller than \(\gamma\), we shouldn’t add that branch (it’ll be negative).

Further prevention of overfitting

XGBoost also uses two additional methods¹ to prevent overfitting:

• Shrinkage: scales newly added weights by a factor \(\eta\) after each step of tree boosting.
• Column (feature) sub-sampling: randomly select a subset of features for each tree (or split), so not all features are available when finding best split. This also speeds up computations of the parallel algorithm.

Shrinkage is similar to learning rate. It reduces the influence of each individual tree, so future trees can improve the model.

1. besides the regularization term

Making it scalable

• Exact greedy algorithm is impossible to do efficiently when the data doesn’t entirely fit in memory - or when in a distributed setting.
• Solution: the approximate algorithm.
• It finds split points for continuous features by using histogram to approximate quantiles of the data distribution
• Don’t consider every feature value, just the boundary values as potential splits
• Uses weighted quantile sketches to determine the bin boundaries

The histrogram basically buckets ranges of similar continuous values so we only have to consider the boundary values.

The weighted quantile sketches:

1. Sort and weigh - sort by feature value, associate each point with a weight
2. Construct sketch in a distributed fashion. A sketch is like a ‘summary’ of the data distribution. Different partitions of the data build local sketches which are then merged together to get a global sketch.
3. Approximate quantiles by using the sketch, and so the weighted quantiles become the candidate split points.

Sparsity-aware Split Finding

• Handle sparse data by adding default directions to each tree node.
• This also exploits the sparsity to make computation complexity linear with non-missing entries in input
  • This lead to 50x speedup over naive version

Block Structures for Parallel Learning

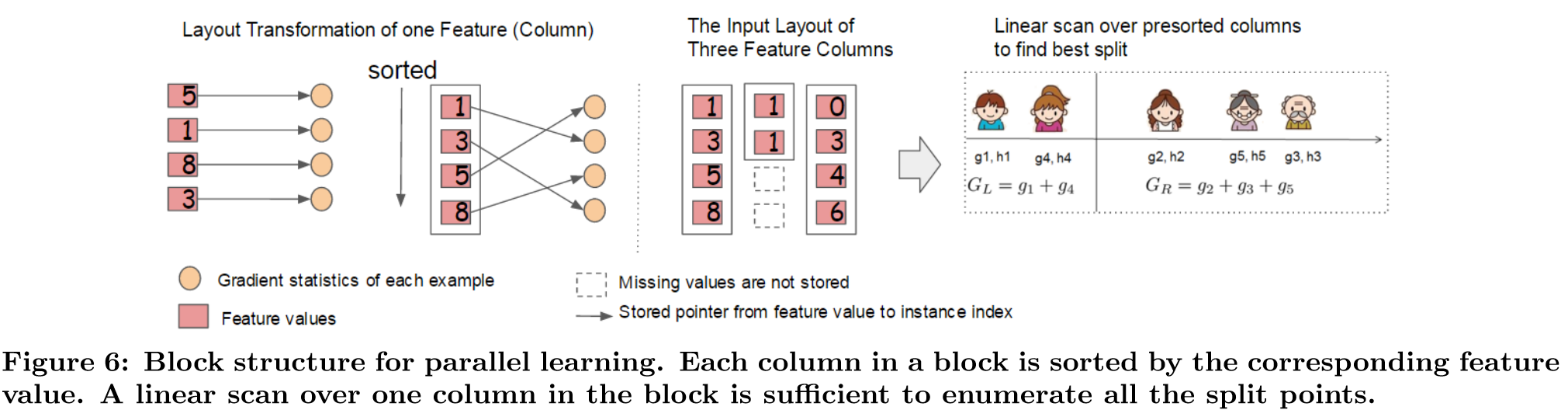
Chen and Guestrin (2016)

• Sorting the data takes most time
• Reduce cost by storing data in (in-memory) blocks
• Stored in compressed column (CSC) format - each column is sorted by corresponding feature vaue

• For exact greedy: store dataset in one block, then only need to do one scan over the pre-sortedentries to get statistics for split candidates
• Approximate algorithm: use multiple blocks - can distribute over machines.
• Easily supports column sub-sampling - just select a subset of columns
• Can parallelize collection of statistics, so we get a parallel algorithm for split finding

Cache-aware access

• Block structure helps computation complexity of split finding, but the new algorithm requires non-continuous memory access
• Want to get cache hits
• Solution: Use prefetching
• Cache-aware algorithm implementation of the exact greedy algorithm runs 2x fast as naive version for large datasets
• For the approximate algorithm, the problem is solved by using a correct block size

Basically, as the algorithm processes each feature, it prefetches the next feature’s data. By the time the algorithm is ready to work on the next feature, the data is already in the cache.

The prefetch mechanism reduces the chance of a cache miss, which would result in a slower fetch from main ram.

Select a good block size which balances parallelization and cache property (too small = threads get too little work, too large = cache misses as gradient statistics don’t fit in CPU cache).

Blocks for Out-of-core Computation

• Can make the system even more performant by better utilizing disk space to handle data that doesn’t fit in main memory
• Divide data into multiple blocks - store them on disk
• Use independent thread to pre-fetch the block into main memory buffer, so computation & disk reading happens concurrently
• Also uses block compression and block sharding

But the independent pre-fetch thread is not enough! Disk reading takes most of the computation time.

We also need to reduce overhead and increase throughput of disk IO. They use two techniques for this:

• Block Compression: block is compressed by columns, and decompressed on the fly via independent thread when loaded into main memory. This helps trade some of the computation in decompression with the disk reading cost.
• Block Sharding: Shard data onto multiple disk in an alternative manner. A pre-fetcher thread is assigned to each disk and fetches the data into an in-memory buffer. The training thread then alternatively reads the data from each buffer. This helps increase the throughput of disk reading when multiple disks are available.

Conclusion

Two Strong Points of the Article

• True end-to-end system optimization. Very impressive focus on creating a scalable, performant system on all levels: distributed hardware, hardware, software, and algorithm.
• Impressive flexibility, enabled by accepting arbitrary loss functions: can do regression, classification, ranking, etc. with XGBoost.

Two Weak Points of the Article

• Evaluation was very focused on efficiency. Would have liked to see more about performance on various tasks.¹
• The focus on so many different optimizations makes the paper very broad

1. Although due to the many awards and challenges won with XGBoost, this is evidently good

Take-Home Message

• Why XGBoost?
  • Superior predictions to many other algorithms, especially on tabular data
  • Incredibly efficient end-to-end system
• And hopefully every word of “XGBoost: A Scalable Tree Boosting System” now makes sense

Chen, Tianqi, and Carlos Guestrin. 2016. “XGBoost: A Scalable Tree Boosting System.” In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 785–94. KDD ’16. New York, NY, USA: Association for Computing Machinery. https://doi.org/10.1145/2939672.2939785.

Friedman, Jerome H. 2001. “Greedy Function Approximation: A Gradient Boosting Machine.” The Annals of Statistics 29 (5): 1189–1232. https://doi.org/10.1214/aos/1013203451.